BLOQUES DE MATEMATICAS 1,2 y 3

TEOREMA DE PARES DE ÁNGULOS

Concepto Ángulo: podemos decir que un ángulo es la inclinación recíproca de dos líneas que se hallan una a otra en un plano y no están ubicadas en línea recta.

Pares de ángulos: Existen unas cuantas variedades de pares de ángulos, en rectas que se cortan, en polígonos, en rectas paralelas cortadas por una secante, en las circunferencias, entre otros, pero entre ellos hay diversas relaciones desde igualdad hasta otras propiedades de acuerdo al resultado de su suma.

 CLASIFICACIÓN POR PARES DE ÁNGULOS

ÁNGULOS ADYACENTES: Son los que están formados de manera que un lado es común y los otros dos lados pertenecen a la misma recta.

 ÁNGULOS COMPLEMENTARIOS: Son dos ángulos que sumados valen un ángulo recto, es decir, 90º.

ÁNGULOS SUPLEMENTARIOS: Son los ángulos que sumados valen dos ángulos rectos, es decir, 180º.

ÁNGULOS OPUESTOS POR EL VÉRTICE: Son dos ángulos tales que los lados de uno de ellos son las prolongaciones de los lados del otro.

 

TEOREMA DE RECTAS PARALELAS Y UNA SECANTE

 

Una recta transversal, es aquella que intersecta a dos o más rectas. Cuando intersecta rectas perpendiculares, entonces se crean varios ángulos congruentes.

ANGULOS ALTERNOS INTERNOS: Son dos ángulos interiores con diferentes vértices en lados opuestos de la transversal.

 

ANGULOS ALTERNOS EXTERNOS: Son dos ángulos exteriores con diferentes vértices en lados opuestos de la transversal.

 

ANGULOS CORRESPONDIENTES: Los ángulos correspondientes están en el mismo lado de la transversal. Uno de los ángulos es un Angulo exterior, el otro es un Angulo interior.

TEOREMA DE ANGULOS INTERIORES Y EXTERIORES DE UN TRIANGULO

Teorema para ángulos internos de un triángulo: Los ángulos internos de todo triángulo suman 180°.

 

Teorema para ángulos externos de un triángulo: Un ángulo externo de un triángulo es igual a la suma de los ángulos internos no adyacentes.

 

 

TEOREMA DE CONGRUENCIA DE TRIÁNGULOS

 

Se dice que un Δ ABC es congruente con otro Δ DEF  si sus lados respectivos son iguales y sus ángulos respectivos también lo son.

Al observar los triángulos de la figura puede apreciarse que tienen lados respectivamente congruentes, que son:

 

También tienen ángulos respectivamente congruentes:

  

CONGRUENCIA DE TRIÁNGULOS

los criterios de congruencia corresponden a los postulados y teoremas que enuncian cuáles son las condiciones mínimas que deben reunir dos o más triángulos para que sean congruentes.

Los postulados o criterios básicos de congruencia de triángulos son:

Postulado LAL

LAL significa lado-ángulo-lado.

Dos triángulos son congruentes si tienen dos lados y el ángulo determinado por ellos respectivamente iguales.

 

Postulado ALA

ALA significa ángulo-lado-ángulo.

Dos triángulos son congruentes si tienen dos ángulos y el lado común a ellos, respectivamente, iguales.

Postulado LLA

LLA significa lado-lado-ángulo

Dos triángulos son congruentes si tienen respectivamente iguales dos lados y el ángulo opuesto al mayor de ellos.

Postulado LLL

LLL significa lado-lado-lado.

Dos triángulos son congruentes si tienen sus tres lados respectivamente iguales.

 

 

 

SEMEJANZA DE TRIÁNGULOS  

Primer Criterio:
Dos triángulos son semejantes si tienen dos pares de ángulos respectivamente iguales.

 

Segundo Criterio:
Dos triángulos son semejantes si sus lados son proporcionales.

 

Tercer Criterio:
Dos triángulos son semejantes si tienen un ángulo igual y los lados que lo forman son proporcionales.

 

 

 

      TEOREMA DE TALES

Es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí.

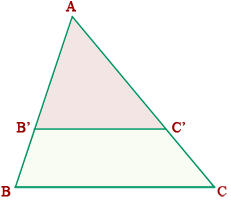
Primer Teorema de Tales en un triángulo:

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.

 

Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.

 Otra variante del Teorema de Tales

 

 

Del primer teorema de Tales se deduce además lo siguiente Si dos rectas cualesquiera (r y s) se cortan por varias rectas paralelas (AA’, BB’, CC’) los segmentos determinados en una de las rectas (AB, BC) son proporcionales a los segmentos correspondientes en la otra (A’B’, B’C’).

 

 


¿OCUPACION DE EL TEOREMA DE TALES EN PROBLEMAS COTIDIANOS?

un poste vertical de 3 metros proyecta una sombra de 1.5 metros; ¿que altura tendrá un árbol que a la misma hora proyecta una sombra de 4 metros
 
aplicando el teorema de tales :

3/x = 1.5/4        de donde      x= 3 * 4 / 1.5 = 8 metros
 
altura del árbol = 8 metros

 

TEOREMA DE PITAGORAS

o    Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.

 

o    En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos

En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. 

a² + b² = c²

Conociendo la hipotenusa y un cateto, podemos calcular el otro cateto.         ¿ocupación del teorema de Pitágoras en la vida cotidiana?  El triangulo entonces queda claramente definido y sabemos que tenemos un cateto que mide 17 km, otro que mide 8 km y que la distancia real que se nos está pidiendo es la hipotenusa del tal triángulo. Aplicamos Teorema de Pitágoras y el planteo sería así: c2 = a2 + b2 c2 = 82 + 172 = 64 + 289 = 353 c = √353 = 18.8